中2数学「後期期末テスト対策問題」

中2数学「後期期末テスト対策問題」となります。
テスト範囲としては
・角度を求める（多角形）
・合同の証明
・確率
となっています。

3学期学年末テスト対策問題（中2数学）

【問1】次の問いに答えなさい。
（1）十角形の内角の和を求めなさい。
（2）内角の和が900°となるのは何角形ですか。
（3）正六角形の1つの外角の大きさを求めなさい。
（4）1つの外角の大きさが30°になるのは、正何角形ですか。
（5）正十角形の1つの内角を求めなさい。

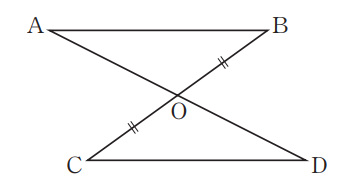
【問2】図において、AB//CD、OB＝OC ならば OA＝OD であることを証明しなさい。

【問3】Ａ，Ｂの２人がじゃんけんを１回するとき，次の各問いに答えなさい。
（1）２人のいし（グー），はさみ（チョキ），かみ（パー）の出し方は全部で何通りあるか答えなさい。
（2）１の出し方はどれも同様に確からしいと考えて，２人があいこになる確率を求めなさい。

【問4】赤と白の２色のカードが２枚ずつ計４枚あり，各色のカードには１，２の数字が１つずつ書いてあります。この４枚のカードをよくきって，１枚ずつ続けて２回ひき，ひいた順に１列に並べます。このとき，次の(1)，(2)の問いに答えなさい。
(1)カードの並び方は全部で何通りありますか。
(2)２枚のカードが色も数字も異なる確率を求めなさい。

【問5】修学旅行で，孝君，洋君，和夫君，明君，信一君の５人は同じ班であるが，ホテルでは，２人部屋と３人部屋に分かれることになった。そこで，次のような方法を考えた。
①５本のうち２本にまる印をつけたくじを準備し，封筒に入れる。
②５人がそれぞれ１本ずつくじを選び，同時にひく。
③●印のついたくじをひいた人が２人部屋，そうでない人が３人部屋とする
このとき、次の問いに答えなさい。
（1）５人の部屋の分かれ方は全部で何通りありますか。
（2）孝君と洋君が同じ部屋になる確率を求めなさい。

3学期学年末テスト対策問題（中2数学）の解答

【問1】
＜今回使う公式集＞
①ｎ多角形の内角の和　　１８０（ｎ－２）°
②ｎ角形の外角の和　　３６０°
③１つの内角＋１つの外角＝１８０°
正ｎ角形において
④1つの外角＝ 360/ｎ角形
⑤1つの内角＝180-1つの外角＝180- （360/ｎ角形）

（1）①の公式より、180（10-2）＝180×8＝1440
（2）①の公式より、180（ｎ-2）＝900　　　　※この問題は、最初に必ず180で割ることで計算が速くなる。
（ｎ-2）＝5
ｎ＝7
（3）④の公式より、360÷6＝60
（4）④の公式より、360÷30＝12
（5）まず一つの外角を求めることが先決！
④の公式より、360÷10＝36°←1つ外角
③の公式より、1つの内角＝180-36＝144°となる。

（解答）
（1）1440°
（2）七角形
（3）60°
（4）十二角形
（5）144°

多角形の内角の和とくれば、180（ｎ-2）、おおよそ全員がすぐ口にできると思いますが、入試では、そのように一筋縄で解ける問題は出題されません。その他に、4つ。すらすらと公式が出てくる必要があります。

【問2】
△OABと△ODCで、
OB=OC…①
∠AOB＝∠DOC…②
AB//CDより、錯角は等しいので∠ABO=∠DCO…③
①，②，③より、1辺とその両端の角がそれぞれ等しいから
△OAB≡△ODCよって、OA＝OD

■三角形の合同の証明の流れ
大きく2つあるのそれぞれ書きます

＜基本型＞
△（　　　　）と△（　　　　）において
（　　　　）＝（　　　　）…①
（　　　　）＝（　　　　）…②
（　　　　）＝（　　　　）…③
①②③より（　　合同条件　　）なので
△（　　　　）≡△（　　　　）

※直角三角形の合同を証明するときの多くは、（　　　　）＝（　　　　）＝90°…①となりますが、直角三角形の合同を証明する問題でも直角三角形の合同条件を使わず三角形の合同条件を使って解く場合も少なくありません。

＜Ａ＝Ｂ＝Ｃの型＞
△（　　　　）と△（　　　　）において
（　　　　）＝（　　　　）…①
（　　　　）＝（　　　　）…②
（　　　　）＝【　　　　】…③
（　　　　）＝【　　　　】…④
③④より（　　　　）＝（　　　　）…⑤
①②⑤より（　　合同条件　　）なので
△（　　　　）≡△（　　　　）
【　　　　】は、90°－∠ＡＣＢなど同じ式になる場合が多いです。

■合同の証明のポイント
三角形の合同の証明は、以上のような流れになりますが、ポイントとしては、問題文を読み、仮定から、どの合同条件が使えるかを予測し、その条件に合うように、等しい辺、角を見つけて、証明していくだけです。

【問3】
まずは、樹形図を描きます。

（2）（1）の樹形図を利用して、場合の数は、9通りで、あいこになるのは3通りなので、3/9となり、1/3

【問4】
「1回戻す」のか、「同時または続けて」なのか。「数字を作るのか、作らないのか」を吟味して、樹形図を描き解きます。4パタ－ンでしたね。
①｢1回戻し｣＋「数字を作る」
②「1回戻し」＋「数字は作らない」
③「同時または続けて」＋「数字を作る」
④「同時または続けて」＋「数字を作らない」
この問題では、③「同時または続けて」＋「数字を作る」となり、以下のような樹形図となる。

以上のようになり、12通り
（2）（1）の樹形図を利用すると、場合の数は、12通りで、２枚のカードが色も数字も異なるのは4通りなので、4/12より、1/3。

【問5】
（1）

2人部屋の組み合わせが決まれば、自動的に残りが3人部屋になるので、樹形図より、10通り。

（2）

樹形図を利用して、場合の数は、10通りで、君と洋君が同じ部屋になるのは、4通りなので、4/10より2/5となる。