高校受験対策・数学「関数の対策問題」です。
関数の対策問題(高校入試数学)
【問1】
下の図のように、原点をOとし、y=ax2のグラフ上に3点A、B、Pがある。3点A、B、Pのx座標はそれぞれ、-2、4、tであり、点Bのy座標は4である。原点Oから直線ABに垂線OHをひく。このとき、次の問いに答えよ。ただし、0<t<4とする。
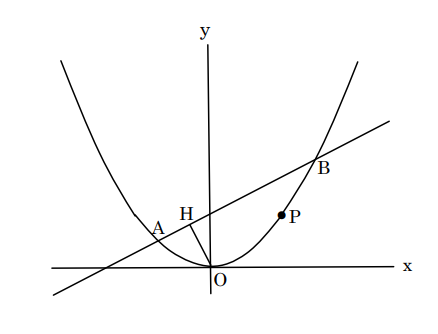
(1)aの値を求めよ。
(2)直線ABの式を求めよ。
(3)線分ABの長さを求めよ。
(4)線分OHの長さを求めよ。
(5)点Pから直線ABに垂線をひき、その交点をQとする。このとき、PQ=OHとなるtの値を求めよ。
【問2】
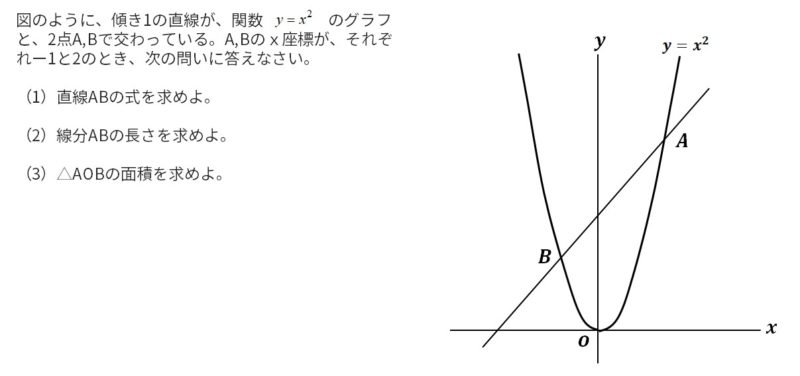
<書き起こし>
図のように、傾き1の直線が、関数y=ax2のグラフと、2点A,Bで交わっている。A,Bのx座標が、それぞれー1と2のとき、次の問いに答えなさい。
(1)直線ABの式を求めよ。
(2)線分ABの長さを求めよ。
(3)△AOBの面積を求めよ。
【問3】
下の図1のような斜面上で、地点Aからボールを矢印の方向に頃が下。ボールが転がり始めてからx秒間に転がる距離ymを調べたところ、 y=1/2x2という関係があった。このとき、次の問いに答えよ。
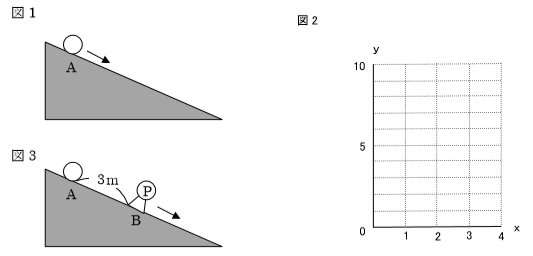
(1)関数y=1/2x2について、xの値が1から3まで増加するときの変化の割合を求めよ。
上の図3のように、地点Aの3m先に地点Bがある。地点Aからボールが転がり始めると同時に、Pさんが地点Bから一定の速さで図の矢印の方向に走り始めるものとする。
このとき、次の問いに答えなさい。
(2)Pさんが走り始めてから6秒後にボールがPさんに追いついたとする。このとき、Pさんの速さは、毎秒何mか。
(3)次に、Pさんは、地点Bから毎秒3mの速さで走り始め、途中で立ち止まった。この1秒後にボールがPさんに追いついた。このとき、Pさんが立ち止まったのは、走り始めて何秒後か。
【問4】
直角三角形ABCにおいて,∠A=90゜,AB=9cm, AC=6cm である。2点P, Qが点Aを同時に出発し, 点Pは線分AB上を毎秒3cmで, 点Qは線分AC上を毎秒1cmで動くものとする。2点P, Qが点Aを出発してからx秒後の△APQの面積をycm2とする。点Pが点Bに到達すると点Qも止まるものとする。このとき次の問いに答えよ。図2は、x秒後の△APQの様子をグラフにしたものである。
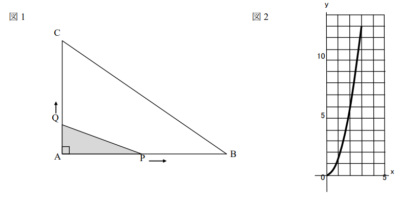
(1)2秒後の△APQの面積を求めよ。
(2) xとy の関係を表す式を求めよ。
(3)△APQの面積が3/2cm2になってから、△APQの面積が△ABCの面積のちょうど半分になるまでにかかる時間を求めよ。
関数の対策問題(高校入試数学)の解答
【問1】
(1)a=1/4
(2)y=1/2x+2
(3)3√5
(4)4√5/5
(5)t=2
【問2】
(1)の解答・解説
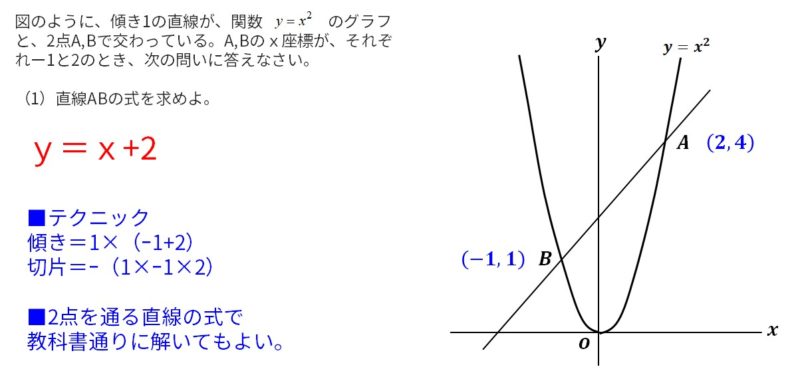
<書き起こし>
■テクニック
傾き=1×(ー1+2)
切片=ー(1×ー1×2)
■2点を通る直線の式なので、連立方程式を使うなどして教科書通りに解いてもよい。
(2)の解答・解説
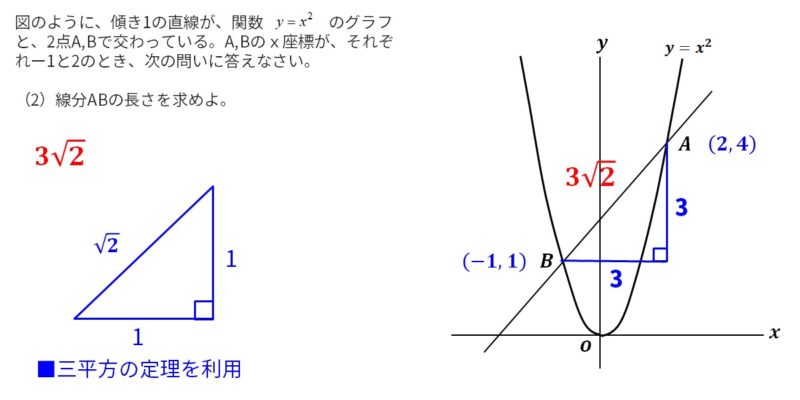
<書き起こし>
■三平方の定理を利用する。また、特別な直角三角形で、1:1:√2を利用する。
(3)の解答・解説

<書き起こし>
関数上の三角形は、上の図示のように解くこともできます。2つの三角形に分け、それぞれ求めて、足してもよい。
【問3】
(1)2
(2)5/2(2.5)
(3)5
【問4】
(1)6
(2)y=3/2×2
(3)2秒後

コメント