中学1年生・数学「頻出の3学期学年末テスト基本問題」

定期テスト対策としての中学1年生・数学「頻出の3学期学年末テスト基本問題」です。

中1数学学年末テスト問題（よく出る編）

問1　次の（　　）にあてはまる語句を下の語群から選び、記号で答えなさい。
（1）直線の一部分で、両端のあるものを（　①　）という。また、（　①　）の長さを2点間の（　②　）という。

（2）円周上の2点を結ぶ線分を（　①　）という。また、円周の一部分を（　②　）という。

（3）直線lと円Oが1点だけを共有するとき、直線lを円Oの（　①　）という。またこのとき、直線lは接点を通る円Oの半径に（　②　）である。

（4）きちんと重ね合わせることができる2つの図形は、（　　　）であるという。

（5）線分を2等分する点をその線分の（　　　）という。

（6）角柱や角すいのように、いくつかの平面で囲まれた立体を（　　　）という。

（7）1つの直線を軸として平面図形を回転させてできる立体を（　　　）という。

問2　次の図形について、次の問いに答えなさい。

（1）線対称な図形をすべて選び、記号で答えななさい。
（2）点対称な図形をすべて選び、記号で答えななさい。

問3　次の問いに答えなさい。
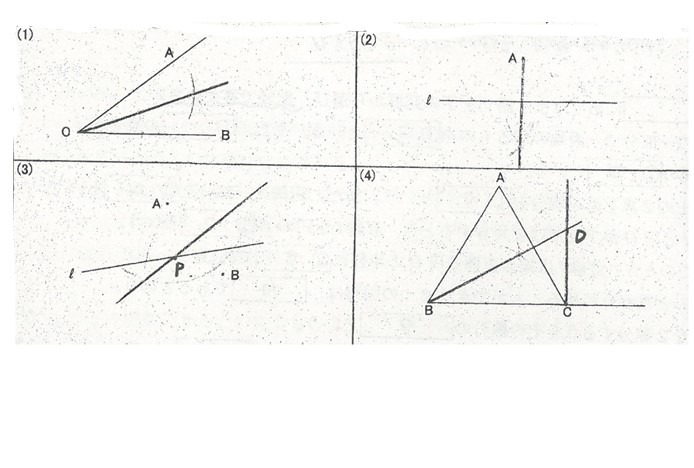
（1）次の図で、∠AOBの二等分線を作図しなさい。

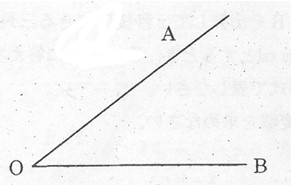
（2）次の図で、点Aを通り、直線lに垂直な作図をしなさい。

（3）次の図で、直線l上にあって、AP＝BPとなる点Pを作図しなさい。

（4）次の図で△ABCは正三角形です。∠DBC＝30°、∠BCD＝90°の直角三角形を作図しなさい。

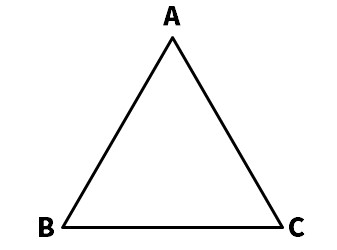
問4　次の図は、合同な直角二等辺三角形を4つしきつめたものです。次の（　　）にあてはまることばを入れなさい。

（1）△FDCは、△EBDを身後の方向にずらした図形と考えられる。このような移動を（　　　）という。

（2）△FADは、△EBDを点Dを中心として時計まわりに90°まわした図形を考えられる。このような移動を（　　）という。

（3）△FADは、△EADを、ADを軸として折り返した図形と考えられる。このような移動を（　　）という。

問5　次の図の直方体について、次の問いに答えなさい。

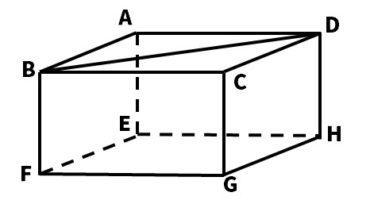
（1）線分BDと面EFGHの関係を記号を使って表しなさい。

（2）辺BCと平行な面をすべて書きなさい。

（3）辺AEとねじれの位置にある辺をすべて書きなさい。

（4）面ABFEと垂直な面をすべて書きなさい。

（5）頂点Aと面EFGHとの距離と等しい長さの辺をすべて書きなさい。

問6　次の立体は、右の㋐～㋓のどの図形を、直線lを軸として1回転させてできたものですか。記号で答えなさい。

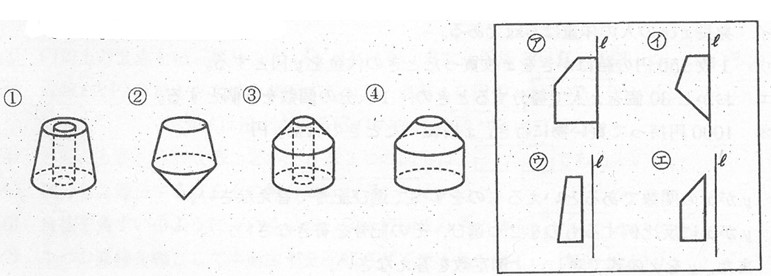
問7　次の投影図で表される立体について答えなさい。

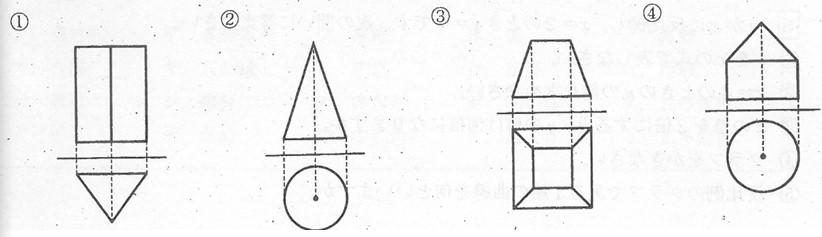
（1）①②の立体の名前を答えなさい。
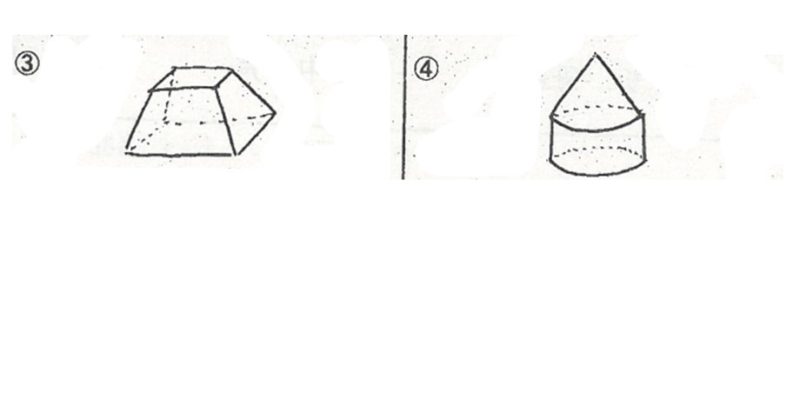
（2）③④の立体の見取図を書きなさい。

問8　次の空間図形に関する問いに答えなさい。
底面の半径が2cm、高さが5cmの円柱の体積と表面積を求めよ。

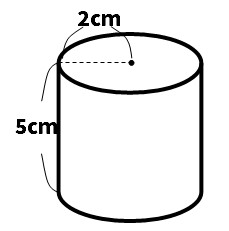
問9 次の図の立方体について，次の問いに答えなさい。

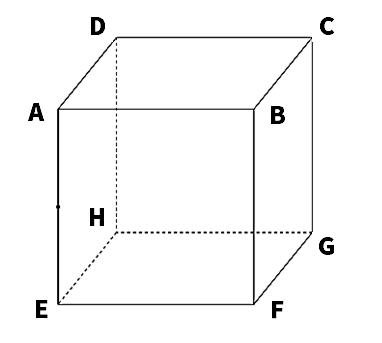
（1）面ABCDと平行な面を答えなさい。
（2）面EFGHと垂直な面はいくつありますか。
（3）面AEHDに平行な辺をすべて答えなさい。
（4）辺AEとねじれの位置にある辺はいくつありますか。

問10 次の表はあるクラスの生徒の身長を度数分布表にまとめたものである。次の問いに答えなさい。

（1）155ｃｍ以上160ｃｍ未満の階級の相対度数を求めよ。
（2）165ｃｍ以上170ｃｍ未満の人の割合を％で求めよ。
（3）中央値を求めよ。
（4）最頻値を求めよ。
（5）平均値を求めよ。

中1数学学年末テスト問題（よく出る編）解答

問1
（1）①シ　②コ
（2）①タ　②エ
（3）①ウ　②サ
（4）カ
（5）ク
（6）イ
（7）セ

問2
（1）㋐㋓㋔
（2）㋐㋑㋓

問3

問4
（1）平行移動
（2）回転移動
（3）対称移動

問5
（1）線分BD//面EFGH
（2）面AEHD、面EFGH
（3）辺BC、辺CD、辺FG、辺GH
（4）面ABCD、面AEHD、面BFGH、面EFGH
（5）辺AE、辺BF、辺CG、辺DH

問6
（1）ウ
（2）イ
（3）エ
（4）ア

問7
（1）三角柱
（2）円すい

（3）（4）

問8 底面の半径が2cm、高さが5cmの円柱の体積と表面積を求めよ。
体積：20πcm³
表面積：28πcm²

問9
（1）面EFGH
（2）4つ
（3）辺BF，辺CG，辺BC，辺FG
（4）4つ

問10
（1）0.25
相対度数＝該当度数（数）÷　全体　※小数で解答する

（2）10％
割合＝相対度数×100（または、相対度数）　※％で聞かれているときに、100をかけます。

（3）157.5
（奇数個の場合）真ん中　（偶数個の場合）（真ん中左＋真ん中右）÷2
〈例〉（奇数個）1、7、8、5、10　の中央値は、小さい順に並び替えて1、5、7、8、10　真ん中にくる7
〈例〉（偶数個）1、7、8、5、10、11の中央値は、小さい順に並び替えて1、5、7、8、10、11であり、
中央値は、（7+8）÷2＝7.5となります。

（4）152.5
最頻値＝もっとも大きな度数に該当する階級値（注1）

（5）156.5
平均値＝〈（階級値×度数）の和　〉÷　全体
（注1）階級値とは、階級の幅の両サイドの数字を足して÷2
（例）　145cm以上～150cm未満　であれば、階級値は、（145＋150）÷2