中3数学「後期期末テスト対策問題」

中3数学「後期期末テスト対策問題」です。
テスト範囲は、
「二次方程式文章題」
「二次関数」
「相似」
「三平方の定理」
「円周角の定理」
となっています。高校入試対策としてもご利用いただけます。
難易度は、「高校入試レベル」となっています。

後期期末テスト対策問題（中3数学）

【問1】次の問いに答えなさい。
図は，ある月のカレンダーである。この中のある数をｘとする。ｘのすぐ真上の数とｘの右どなりの数をかけたものはｘに３を加えた数の９倍したものに等しい。このとき，ｘを求めなさい。ただし，ｘについての方程式をつくり，答えを求めるまでの過程も書きなさい。

【問2】次の問いに答えなさい。
1個50円で売ると、1日に200個売れる商品がある。この商品の値段を1円下げるごとに、1日の売り上げ個数が8個ずつ増える。そこで、1日の売り上げ額を11200円にしたい。この商品の値段をｘ円値下げするものとして、ｘを求めなさい。方程式をつくり、求める過程も書け。ただし、消費税は考えないものとする。

【問3】図1のように、ＡＢ＝ＢＣ＝12ｃｍ、∠ＡＢＣ＝90°の直角二等辺三角形がある。点Ｐは、頂点Ａを出発し、辺ＡＢ、ＢＣ上を通って、頂点Ｃまで毎秒2ｃｍの速さで進み、頂点Ｃで停止する。また、点Ｑは点Ｐが出発すると同時に頂点Ｂを出発し、辺ＢＣ上を通って、頂点Ｃまで毎秒1ｃｍの速さで進み、頂点Ｃで停止する。このとき、点Ｐと点Ｑが同時に出発してからｘ秒後の△ＡＰＱの面積をｙｃｍ2とする。図2は、点Ｐと点Ｑが同時に出発してから頂点Ｃに着くまでのｘとｙの関係をグラフに表したものである。

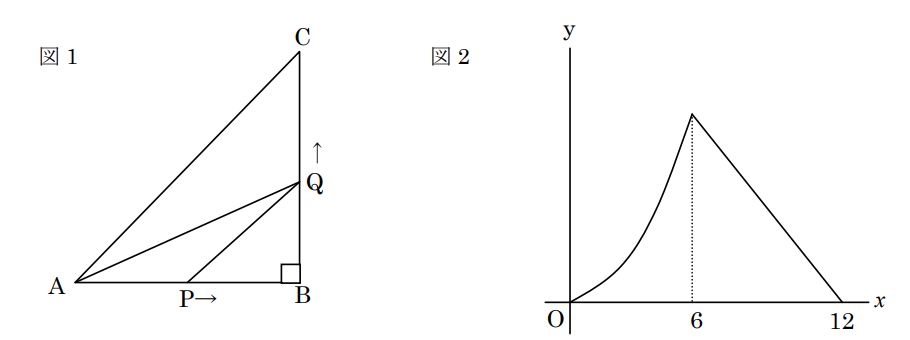
（1）点Ｐと点Ｑが同時に出発してからの3秒後の△ＡＰＱの面積を求めなさい。
（2）ｘの変域が0≦ｘ≦6のとき、ｙをｘの式で表せ。
（3）ｘの変域が6≦ｘ≦12のとき、ｙをｘの式で表せ。
（4）点Ｐが辺ＢＣ上にあるとき、△ＡＰＱの面積と△ＡＰＢの面積が等しくなるのは点Ｐと点Ｑが同時に出発してから何秒後か求めなさい。

【問4】下の図のようには、AB＝8、AC＝6、∠BAC＝60°の△ABCがある。∠BACの二等分線と辺BCの交点をD、点Cを通りADに平行な直線と辺BAの延長の交点をEとする。次の問いに答えよ。

（1）BD：DCをできるだけ簡単な整数比で表しなさい。
（2）△ABDと△ACEの面積の比をできるだけ簡単な比で表しなさい。
（3）辺CEの長さを求めなさい。

【問5】正方形ABCDがある。図のように、頂点Cを中心としおて、半径BCの円をかく。辺AD上に点Ｅを、弧BD上に点Fを、DE=FEとなるようにとり、線分CF,CE,EFを引く。このとき、次の問いに答えなさい。

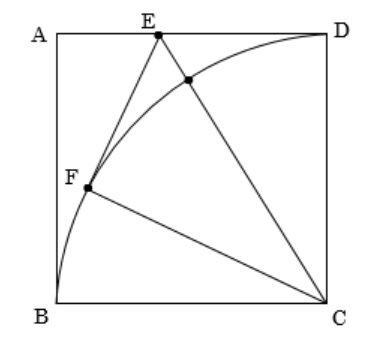
（1）△ＣＤＥと△ＣＦＥが合同であることを証明しなさい。
（2）問題図において、ＣＦ＝4√3、ＤＥ＝4cm、∠ＤＣＥ＝30°のとき、弧ＢＤと線分ＥＦと線分ＤＥに囲まれた部分の面積を求めなさい。

後期期末テスト対策問題（中3数学）の解答

【問1】
「ｘのすぐ真上の数とｘの右どなりの数をかけたもの」で1つ式を作る。…(x-7)(x+1)
「ｘに３を加えた数の９倍したもの」で1つ式を作る。…9(x+3)
それぞれは、「等しい」ので、方程式で解いていく。

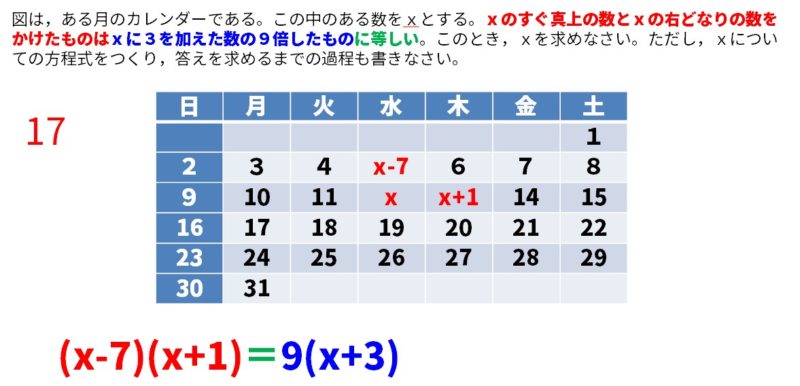
(x-7)(x+1)＝9(x+3)
これを解くと、
x=-2,17
x＞0より
x=17

【問2】
(200+8x)(50-x)=11200
x=10、15　　
これは問題に合う。
（答え）10円または15円

【問3】
（1）9
（2）ｙ＝ｘ2
（3）ｙ＝－6ｘ+72　
（4）8秒後

【問4】
（1）4：3　
角の二等分線定理より、ＡＢ：ＡＣ＝BD：DC＝8：6＝4：3

（2）16：21　

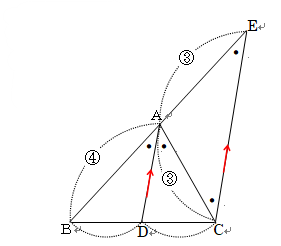
ＢＤ：ＣＤ＝4：3より、面積比△ＡＢＤ：△ＡＣＤ＝4：3…①
相似比4：7である△ＡＢＤ∽ＢＥＣなので面積比△ＡＢＤ：△ＢＥＣ＝16：49…②
①②より、比を合わせる（△ＡＢＤの比が4と16で表せている。）
すると、面積比△ＡＢＤ：△ＡＣＤ＝4：3＝16：12…③
ここで、△ＡＣＥの面積（比で表す）＝△ＢＥＣ－△ＡＢＣ＝49-28＝21となる。
よって、△ABD：△ACE＝16：21

（3）6√3

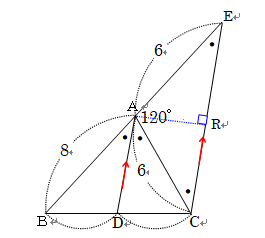
点Ａから線分ＣＥに垂線を下ろした交点をＲすると、△ＡＥＲは、特別な直角三角形
（1：2：√3）
のことにより、ＥＲ＝3√3 となる。
△ＡＣＥは二等辺三角形より、ＣＥ＝2×ＥＲ＝2×3√3＝ 6√3

【問5】
（1）
△CDE と△CFE において
仮定より、DE=FE …①
共通な辺より CE=CE…②
円の半径の長さは、等しいので CD=CF…③
①②③より、3 組の辺がそれぞれ等しいので、
△CDE≡△CFE

（2）16√3-8π
四角形CDEF-おうぎ形CDF